|
C. ALMEDER
Department of Operations Research and System Theory, Vienna University of
Technology, Vienna, Austria
J. P. CAULKINS
Drug Policy Research Center, RAND Corporation, Santa Monica, California,
United States of America
G. FEICHTINGER AND G. TRAGLER
Department of Operations Research and System Theory, Vienna University of
Technology, Vienna, Austria
Abstract
Introduction
Basic aspects of drug initiation models
Descriptive age-specific models of initiation
Optimization of age-specific models of prevention
Conclusion
References
*Research for the present paper was financed in part by the Austrian Science Foundation.
ABSTRACT
The present paper introduces several models concerning drug initiation and drug epidemics that extend traditional single and multi-state dynamic models by explicitly considering the age distribution of users. This age-specificity yields more realistic models, because both human behaviour and the influence of personal relationships can depend on age and the age difference. Furthermore, prevention programmes—especially school-based programmes—can be targeted to reach certain age groups. The models allow the dynamics of drug epidemics to be reproduced in greater detail. The models can be used either for studying the features of drug initiation or for discovering how best to allocate resources to prevention programmes for different age groups.
Models of drug initiation and drug use are often based on the same principles as epidemiological models. At first sight, it is not clear why drug use and infectious diseases have much in common. Initiation into consumption of an illicit drug is usually a deliberate decision of an individual, whereas the act of infection by a pathogenic agent (for example, the common cold virus) usually takes place without the infected individual having any awareness of the process. In contrast to a drug epidemic, most individuals infected by a certain disease undergo the same run of infection, that is, almost all individuals either recover or become immune or remain infected. The process of recovery from drug consumption may differ for different users. It may be a healing process, if the user was addicted, or may result from the user's free choice to quit consumption or from the application of drug enforcement policies [1].
Nevertheless, drug use is clearly contagious in the sense that use by some individuals affects the probability that others will use it through multiple mechanisms. In a very literal sense, most users are introduced to a drug by a friend or relative; the more drug users there are, the more likely an individual is to be offered the drug [2]. At a market level, the larger the market, the more diluted the enforcement risk, and the safer it is to try drugs [3]. At a reputational level, experiences of others can be instrumental in shaping perceptions of the riskiness of drugs, and those perceptions in turn influence initiation [4]. Indeed, the very fact that the mechanism of transmission does not involve physical contact or inter action means that the dynamics of contagion can be more complex and more interesting.
Looking at drug use and the process of initiation in more detail, it is clear that the decision of a non-user to start consumption depends strongly not only on the immediate, personal social environment of the person concerned, but also on the overall reputation of a drug in society, for example, as portrayed in movies or news media. Therefore, a person might want to use drugs even though none of that person's associates encourages the desire. Conversely, a person may fear drugs even if no one that he or she knows has suffered harm from them.
The foregoing rough explanation already shows the complexity of drug initiation and the large number of parameters influencing the process. The complexity grows if the age dependency of those factors is taken into consideration. The disadvantages of complex models stem from the lack of data for parameter identification and the difficulties in analysing them. Hence, in the present paper, as age dependency is introduced into models of drug use, an effort will be made to keep other aspects of the models relatively simple.
More specifically, the additional insight considered and quantified in the pre sent paper is that the influence of a drug user on a non-user vulnerable to initiation can depend on the ages of both persons. A 16-year-old might look up to and seek to emulate an 18-year-old, but rebel and try to do exactly the opposite of what his or her parent's generation is perceived to be doing. So drug use by an 18-year-old might encourage a 16-year-old to initiate use, even though drug use by a 38-year-old might discourage it. Or perhaps for some drugs and some situations, use by a 38-year-old is a stronger endorsement than is use by an 18-year-old. Which ever scenario is considered likely, there is no way to incorporate such effects into existing models. There are age-specific epidemiological models in the literature [5–6], but, as mentioned above, the process of contagion is different for drug initiation. Therefore, those models are not capable of describing the dynamics of a drug epidemic. The present paper describes a new class of models that can consider such effects in an explicit quantitative framework and gives some initial results. Furthermore, control models of prevention, which are based on the descriptive age-specific drug initiation models, are introduced.
First of all, a very general description of the basic features of drug initiation models is given. Those features are the foundation for the further development of initiation models towards age-structured models, which are presented below (see “Descriptive age-specific models of initiation”). Some heterogeneity is already introduced by dividing the population into multiple groups (see “Multi-state models” below), but that is qualitatively different from the models, introduced later, with an infinite number or continuous distribution of states.
The simplest model of drug use in a population distinguishes only between
persons who do not consume drugs and those who do. It is common in such models
to ignore variation in the overall population size. That means that the number
of deaths is equal to the number of births. In that case, the only things
to consider are the flows from the non-user group to the user group and back
(see figure I). The flow from the non-user to the user group—the initiation
rate—is influenced by several factors, including the following:
Figure I. Simple user--non-user model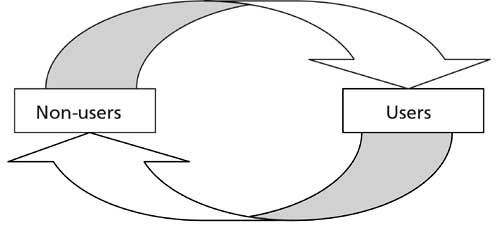 |
(a) A basic initiation rate representing the probability that a non-user starts drug consumption without any influence from others. The basic initiation rate is drug-specific, but also culture-specific. Therefore, different initiation rates must be considered not only for different drugs, but also for different cultural contexts. Apart from that, the basic initiation rate may also depend on time (in the United States of America, for example, there were higher basic initiation rates for cocaine during the late 1960s than during the early 1950s);
(b) The reputation of the drug in the society. Reputation is determined by the number of drug consumers, but it is not necessarily the case that more drug users always mean a more favourable reputation. For some drugs, there could be a threshold. Beneath that threshold, the reputation increases with the number of users, but above the threshold, it decreases because a very high number of drug users could underscore the problems caused by drug consumption;
(c) The effect of prevention programmes. Prevention programmes can re duce the initiation rate, but only down to a certain level. Unfortunately, no programme can reach all people, and not all people reached change their behaviour.
The flow from the user group to the non-user group also involves the following different factors:
(a) The flow implied by the assumption of zero population growth (if all newborns are assumed to be in the non-user group, then there must be a flow from the user to the non-user group representing the death of users and their replacement by newborns who are not users);
(b) A basic rate at which drug users stop their consumption;
(c) The effect of treatment. With more treatment the flow from users to non-users is increased, but only up to a certain threshold (similar to the effects of prevention programmes on the initiation rate).
Note that if the user group represents all people who have consumed drugs at least once in their lifetime, then the flow from the user to the non-user group consists only of the part due to the zero population growth.
When considering models with a constant population size, it is necessary to analyse only one of the groups; all individuals who are not in that group must be, by definition, in the other. The dynamics of the model therefore depends only on one state, and the analysis becomes accordingly simpler.
One type of a more detailed model distinguishes not only between drug users and non-users, but also between different kinds of users and possibly also between different kinds of non-users. Such a multi-state model is explained by Everingham and Rydell [7], who divide users into groups of light and heavy users. The light drug users consume drugs at most once per week; the heavy users consume several times per week or more often.
Even that simple binary distinction generated many insights, but there are other ways of splitting the population in multiple groups. A principle constraint on such elaborations is data availability. For example, if there is no distinction in the data between the amounts used and the frequency with which people use drugs, then it makes no sense to introduce different levels of drug consumption into the models.
Although the population is split into several groups,
they can all be combined again into two sets of groups, namely those groups
representing the non-user popu lation and those representing the drug consumers
(see figure II). Some examples of groups within the non-user population are:
general non-users; non-users who have been exposed to a prevention programme;
and former users. Examples of groups within the user population are: light
users; heavy users; and users under treatment.
Figure II. Multi-stage model with subgroups of users and
non-users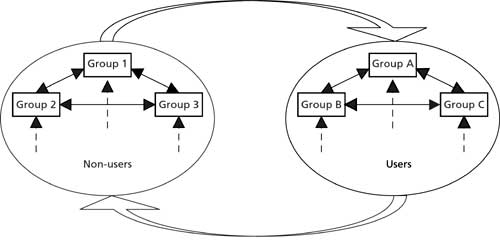 |
In the multi-state models, there are not only transitions between non-users
and users, but also within those groups, for example, from light users to
heavy users. Very complex models can be generated with many different states,
but, as mentioned above, it is only useful to develop a model that can be
supported by the available data. Highly differentiated data acquisition allows
modelling of drug dynamics in greater detail.
The central contribution of the present paper is to introduce another form of heterogeneity to the models, specifically to take into consideration the age of the individuals. Such an extension yields much more realistic models, because it is certainly true that behaviour can depend on age. For example, people between 13 and 25 years of age are much more likely to start drug consumption than are people over 40. It is also true that not all people have the same influence on a person of a certain age. That influence can depend on their age and the age difference. Furthermore, prevention programmes—especially school-based programmes—can be targeted to reach certain age groups. Therefore, such an extension is useful, although the increased complexity makes it much more difficult to analyse such models and gain practical results [8].
A simple way to introduce age is to split the population into different age groups. That leads to so-called compartment models, such as those described above (see “Multi-state models”), but with a large number of population groups [9]. A more general method is to include age as a second parameter in addition to time. A continuous age distribution of the population can then be fully considered. The analysis of the model becomes in some way easier, because there are fewer groups to consider, but in some sense also more complicated, because the method leads to a system of partial differential equations—a further development of the so-called McKendrick equation [10].
As a first step, the simplest model with 2 groups (that is, non-users and users) is extended to consider age-specific reputational feedback on initiation. The details of the underlying model change a little. It is assumed that there is a fixed birth cohort size, which moves only into the non-user group at age 12 (that is, any use before the age of 12 is ignored). There are no deaths during the sub-sequent lifetime of 60 years, so that all individuals live from age 12 to age 72. Then they are removed from the model, either by death or because they are presumed no longer to affect drug use. In addition, it is assumed that there is no recovery from drug use, so that the backflow from users to non-users can be neglected (see figure III). Since people obviously do cease drug use, the practical implication of the simplification is that the pool of users is more properly understood to be the pool of those who ever used drugs, not the pool of current or past-year users.
Figure III. Schematic representation of a simple
age-specific model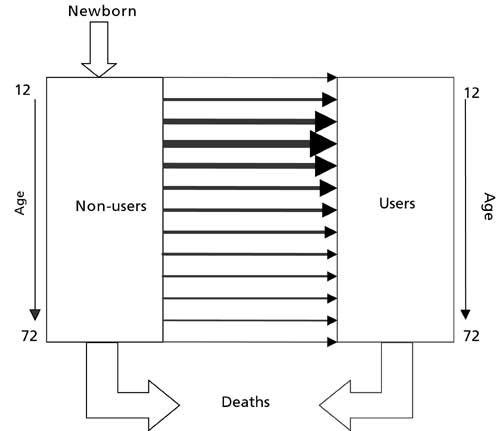 Note: Thicker arrows indicate higher initiation rates |
The initiation rate involves three factors (see “Homogeneous modelling
of the population—single-state model” above), namely the basic initiation
rate, the reputation of the drug and the effect of prevention programmes.
Each factor depends on age. Prevention programmes always suppress initiation,
but the reputation effect can influence initiation in either direction (see
figure IV).
Figure IV. Influences on the initiation rate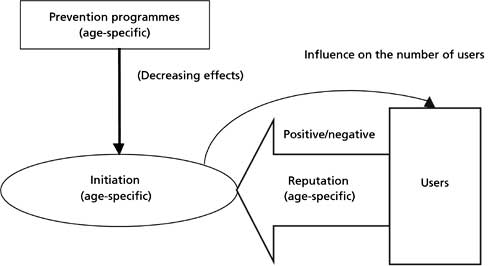 |
In the simpler model
without age differentiation, the reputation was construed as an overall image
held by the society as a whole, but a more differentiated view is now adopted
because the reputation is age-specific. In other words, at any given point
in the drug epidemic, people of different ages can have different perceptions
of the drug. Furthermore, the influence of a given user on someone else's
perceptions of the drug can depend on age and the age difference. So the
main factor for the reputation is how much influence a user of age
b has
on a non-user of age
a , and
whether the influence is positive or negative. Such a relationship can be
a socially- or culturally-specific factor. The authors believe that, at least
for the typical drug in North America or western Europe, such influence may
be described as follows:
(a) Young people are more sensitive to peer pressure, so that the older a non-user is, the weaker the influence of any other user on that individual;
(b) The influence depends primarily on the age difference between the user and non-user;
(c) Especially for young non-users (who have the highest underlying proclivity to initiate drug use):
(i) Persons who are of the same age or a little older set examples, and their influence is therefore very high;
(ii) Persons who belong to their parents' generation may evoke a contrarian response, or at least have only a small impact, and therefore a very low and possibly even a negative influence.
The reputation of the drug that is effective on a non-user of age a is the compound influence of the users over all ages.
The feedback from considering the influence of users on the initiation rate of non-users can generate very interesting behaviour in the model. The drug users never vanish completely, because neither a low reputation, nor an expensive prevention programme can reduce initiation to zero. In most cases, when no prevention programme is applied, the number of users becomes stabilized and reaches an endemic equilibrium. On the other hand, it is also possible to end up with an oscillation of repeated waves of drug use, if the influence of the parents' generation is negative.
The intuitive explanation for the modelled behaviour
is the following. If there are few older drug users, then their negative
influence on the younger potential users is very small. Therefore, initiation
of new drug users at younger ages is high (initiation by older individuals
is low and relatively insensitive to use by others). Some years later, those
former young drug users grow older and cause a strong negative reputation
of the drug for the new young non-users. That keeps the initiation rate very
low and results in a large non-user group in younger and eventually middle
ages. The older users eventually disappear, which reduces their negative
influence on initiation, and the cycle can begin again.
Figure V. Oscillation in the non-user population due to
the negative influence of the parents' generation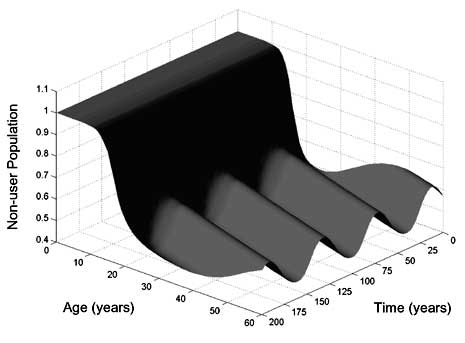 Note: The results are based on data on marijuana initiation in the United States . The user group represents those people who have consumed marijuana at least once in their lifetime |
Figure V shows the cycles graphically. In particular,
it plots, as a function of time, the proportion of an age cohort that has
never used drugs. Troughs in the graph represent peaks in use because everyone
is either a user or a non-user. People in the youngest age groups are primarily
non-users at all times, as is indicated by the plateau in the graph for those
ages. Initiation occurs primarily in the adolescent years (indicated by the
cliff at those ages), but the ultimate lifetime prevalence of drug use varies
from birth cohort to birth cohort (indicated by the series of ridges). The
time differences between peaks of drug use are about one to two generations,
depending on the influence of users on non-users. The amplitude is about
10 to 20 per cent of a birth cohort size.
As mentioned before, the reputation factor depends strongly on the social structure, that is, it may have completely different forms for drug epidemics in other countries or times. The example shows, however, that a model with just one state but a heterogeneous age structure can produce cycles of drug use of the type observed historically [11]. Furthermore, such cycling is not the only possible outcome. It is therefore possible to explore conditions under which cycling occurs and contrast them with conditions under which drug use approaches a constant steady state. Still more complex behaviour can be obtained by further refining the state space, as discussed below.
One way to refine the model
described above is by splitting the user and non-user groups into subgroups
as shown above (see “Multi-state models”). Following the lead of Everingham
and Rydell [7] and Behrens and others [12], a distinction is made between
light and heavy users. That yields three population groups consisting of
non-users, light users and heavy users [13]. A key motivation for the distinction
is the assumption that light users, who may be using the drug for recreational
reasons, can create a positive impression of the benefits of drug use, whereas
the heavy or addicted users who manifest the adverse effects of drug use
create a negative impression. Hence, the underlying assumption of the model
is that the more light users there are, the better the reputation of the
drug is, but the more heavy users there are, the worse the drug's reputation
and, hence, the lower the initiation rate (see figure VI).
Figure VI. Schematic diagram of an age-specific
L-H-model Note: Thicker arrows indicate higher initiation and transition rates |
As the model includes age, the reputation is age-specific
and the main factor is again the impact of light and heavy users of age
a on the
initiation rate of a non-user aged
b . A big
influence is assumed if the age difference is small, and a small impact if
the age difference is large, which reflects the fact that people have more
social contacts within their own age group than with other age groups.
Similar to the model discussed above (see “Age-specific single-state models”), the L-H-model shows different types of behaviour depending on the magnitude of the negative influence of heavy users on reputation. If the negative influence is very small, then drug use converges to a single, high equilibrium level of drug use. If it is very large, then initiation is uniformly low and use converges to a single, low equilibrium level. However, if the influence of heavy users is in a moderate range, the model produces cycles of greater and lesser drug use [13]. Intuitively, the reason is about the same as for the model presented above (see “Age-specific single-state models”). A high number of heavy users reduces the initiation rate for younger non-users, but as they grow older and disappear, their negative impact wanes and a new wave of drug consumers is created, which results later on in a high number of heavy users again.
As mentioned above (see “Multi-state models”), that is only one way to extend the model. Other groups can be included as long as data are available for estimating the age-specific transition rates between those groups.
The models discussed above were descriptive. Their main contribution was to show how age-specific reputational effects can generate cycles of greater and lesser drug use. From a policy perspective, the aim is not only to describe drug, but also to control them. Since resources are always constrained, a common and fruitful question is to ask how drug control interventions should be managed in order to achieve some reduction in use at the least possible cost.
There is an emerging literature on resource allocation questions, but to date much has focused on trading off spending on different types of interventions (for example, treatment versus enforcement [14-15]), or trading off interventions at different points in a drug control epidemic [16-17], or trading off the benefits of attacking different local markets [18-19]. For school-based prevention programmes, another interesting variant of the question pertains to the appropriate age at which to intervene.
By and large enforcement and treatment interventions cannot be age-specific. Different sanctions can be imposed on juvenile and adult offenders, and treatment policies that are contingent on the number of past treatment episodes have some power of age discrimination, but for school-based drug prevention the ability to target particular ages is much greater. Except for the extent to which students skip or fail grades, there is almost a one-to-one mapping between grade level and age. It can therefore be asked at which grade (age) should most school-based intervention efforts be targeted.
The question is in fact complex and multifaceted. In theory, the preference would be to factor in differential school attendance by age (due to dropping out and truancy) and how intervention varies in effectiveness with age. Consideration is here given to just a subset of those issues that cannot be analysed directly without an age-heterogeneous model. How should the fact that baseline initiation rates vary over time, and that past initiates can promote further initiation, in particular of people from the same birth cohort, affect the ages of intervention?
To address that question, the previously introduced
models are converted into an optimal dynamic control formulation [13]. A
variety of objectives can be considered, for example, the total costs of
drug use, including the social costs caused by the drug consumers and the
costs of running the prevention programmes themselves. Initially, it was
assumed that a prevention programme only affects the initiation rate while
the programme is being run. When the programme is stopped, the initiation
rate immediately returns to the rate that would have pertained in the absence
of any prevention programme. For that simple case, in which the prevention
programmes have no memory effects, the results are predictable. In general,
expenditures should be directed to the age classes with the highest initiation
rates (see figure VII). However, the spending profile does not match the
initiation profile exactly. Because of the contagious character of drug use,
prevention interventions should be shifted somewhat towards younger ages.
Figure VII. Basic initiation rates and prevention
programmes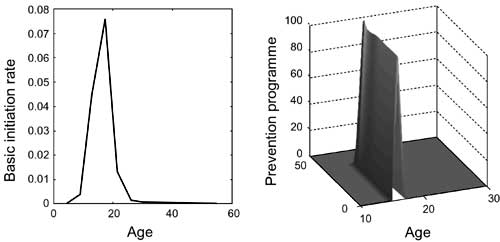 Note: The graph on the left shows the age-specific basic initiation rate, which was used for the calculations. The graph on the right shows a typical result for an age-specific prevention programme without a memory effect. The small age range of the prevention programme emerges from the relatively low social costs of drug users. Assuming higher social costs provokes a wider age range |
One way to include prevention programmes with a memory
effect is to split the non-users group into two parts, a group of people
who have already taken part in a prevention programme, and another group
that has not. So the implementation of a prevention programme results in
a flow from one of those groups into another. A backwards flow could be included
to represent forgetting or a decay in the effects of the programme. People
who have taken part in a prevention programme would presumably be modelled
as having a reduced drug initiation rate compared to those who have not taken
part. Such a model can be compared to some extent with vaccination models,
where the vaccinated part of the population is in one group. After some time,
the vaccination effects fade away and people are again susceptible to infection.
The model falls into the class discussed above (see “Age-specific multi-state models”), and for such a prevention programme an optimization can be performed with regard to some objective. Hence, the most important age classes for applying a prevention programme can be calculated, so that the best effects can be obtained (the analysis of the optimal control models is currently under way).
Introducing age-specific aspects into drug initiation models allows the development of more complex models that give detailed insight into the underlying processes of drug epidemics and their control. The simple single-state model discussed above (see “Age-specific single-state models”) already shows a big advantage of age-structured models: the complex dynamics of a drug epidemic can be simulated using a model based on simple, manageable assumptions, such as distinguishing between just two groups of people. The behaviour of the solution (cycles or constant equilibrium) depends on the type of age-specific feedback. To gain similar results with traditional multi-state models that do not differentiate by age, a larger number of groups would be necessary.
In particular, the age-specific concept allows the incorporation of an age-specific reputation effect (feedback from the number of users on the initiation rate), which depends on how much influence a user of age b has on a non-user of age a , and whether that influence is positive or negative.
Another advantage of age-specificity is the ability to investigate age-structured strategies for prevention and to optimize them. Although only programmes without a memory effect are addressed above (see “Optimization of age-specific models of prevention”), the extension to other types of prevention is straightforward and fits into the scope of models presented in the present paper. Such an investigation is currently the main focus of concern.
Many issues concerning population dynamics include heterogeneity, either spatial or temporal. The age distribution of a population can change sometimes very quickly, and can be completely different in different regions. Hence, it is necessary that a model for adapting strategies to the different cases should incorporate the age distribution of population groups. The age-specific models presented in the present paper are a first step towards including more heterogeneity in drug epidemic models. Further extensions would be to use finer group classifications or to introduce the duration of use as a third parameter, because some aspects of drug initiation depend on how long an individual has been in his or her current group. For example, the probability of an individual moving from light to heavy use may be related to the duration of his or her drug consumption. Theoretically, such an extension can be developed from the models discussed in the present paper, but, in the current state of science, the analysis of those models encounters difficulties on two sides: the availability of data for the large number of parameters and the numerical limitation due to computational power.
In summary, the age-specific models described in the present paper allow more detailed insight into the dynamics of drug epidemics. By formulating them as optimal control models, they can be used to increase the effectiveness of prevention programmes through improved targeting.
|